Generating irregular words from a root



Next: Generating regular forms
Up: Implementing morphological generation within the MA
Previous: The exported routines
Irregular words are those which don't obey the normal rules of
inflection. In English, these are mainly strong verbs: sing/sang/sung. Smaller classes of irregulars include nouns such as
mouse/mice and child/children, and pronouns such
as I/me.
The problem then is that we are given the root form of a word. This is
the uninflected form: the infinitive of a verb, the singular of a noun,
the nominative case of a pronoun. We also have a feature-set which
specifies some syntactic attributes, such as plural or past tense. Given
these two, we want to generate the correct irregular form.
Note that there are problems with the roots of compound words such as
motherhood or house-boat, and I shall only discuss simple
words here. Compound words are dealt with in
section 3.3.6, which also describes how the roots are
obtained.
The MA lexicon holds entries for irregular forms. It turns out that
each entry has room to store the root form too. So there is enough
information in the lexicon to go back from roots to irregulars, and the
problem reduces to one of efficient indexing. It is necessary to know
something about how the lexicon is stored, and I'll describe that next.
This section and the next go into a lot of implementation details about
how the MA stores lexica. First time round, you may want to skim them,
and skip to section 3.2.5, which gives an abstract
specification of the irregular form generation problem.
When you write a lexicon, you write it as a sequence of lists, each
representing one lexical entry. Each entry has five fields:
- Citation field. This holds the surface form of the word. It is
usually in lower-case, though I have seen partially-capitalised fields
such as
Kim and French-polish. I do not know whether this
is essential to indicate how the surface form should be capitalised: I
think we still have to decide how that is best done.
- Phonological field. This is intended for information about
pronunciation: it could for example store the pronunciation in Alvey
Speech Club form. In the current lexicon, it is usually a null string,
though it sometimes duplicates the citation field. It is completely
irrelevant to the Assistant as implemented so far, but might be useful
to help it suggest corrections for frequently-confused homophones, such
as hear/here.
- Syntactic field. This holds a feature-set describing the word's
syntactic properties.
- Semantic field. The MA's original implementors intended this for
information about the meaning of a word. We have decided to use it to
hold the root form, so the entry for sung would have to contain
sing in this field: see section 3.2.7. I have seen some
MA lexica where this field contains not a root but some kind of
meaning-representation; but I shall assume in future that we will always
have a root here.
- User field. This is intended for anything else the user wants to
throw in. In the current lexicon, it is always NIL.
As examples, here are three lexical entries, as written into the
source text of the lexicon:
(abbot "" (N (COUNT +)) ABBOT ())
(abandon "" (V (ARITY 2) (LAT -) (SUBCAT NP)) ABANDON ())
(+s +s ((FIX SUF) (V +) (N -) (FIN +) (PAST -) (AFFREG +)
(AGR ((BAR 2)(V +)(N -)(FIN +)(SUBJ +)))
(STEM ((V +)(N -)(INFL +)
(AGR ((BAR 2)(V +)(N -)(FIN +)(SUBJ +))))))
S NIL
)
In these, the feature set for abbot is
(N (COUNT +))
The initial N is itself a shorthand for the feature set
( (BAR 0) (V -) (N +) )
and is declared as such in an Alias N declaration in the file
decls, one of the declaration files containing feature names and
other things needed by the lexicon. With that expanded out, the feature
set for abbot becomes
( (BAR 0) (V -) (N +) (COUNT +) )
This is exactly the same as the internal representation used in the MA.
As mentioned in the introduction, an MA feature set is represented as a
list of lists. Each of the internal lists has two elements: the first
being a feature name, and the second being a value. Feature sets can
also be written in square bracket notation. I haven't seen any lexical
entries that use this, but a number of the declarations, and all the
word-grammar rules, do.
The format of the lexicon source file is described in section 8 of
[MA].
In this section, I describe how the lexicon is stored and accessed
internally.
Before the lexicon can be used by the MA, it has to be ``compiled''.
This entails calling the MA routine D-MakeLexicon, which builds
two files. One of these is a tree-structured index to the entries,
designed for efficient lookup given a string of characters. The other is
the entries file itself. For a lexicon called d-le, the index
would go into a file called d-le.ma, and the entries themselves
would go into d-en.ma.

The entries file generated by D-MakeLexicon is, like the source
text, a sequence of lists, one for each entry. The index file is a
``trie'', a standard data-structure for efficient lookup on strings
([Sedgewick], [Wood]). Each leaf of the tree contains an
integer, which is the position in the entries file of the corresponding
lexical entry. This position is calculated by the Lisp function
file-position. Note: this is when the ``in-core'' flag is off,
its normal setting. Some systems will only work with it on, see
section 3.2.3 for what happens in that case. As well as the
index, the index-file also contains a few other bits and pieces at the
beginning and end.
The first part of an index file is shown below:
(CL 3 0 UU)
(
|virreg-en.ma|
(
+
(
|a|
(|b| (|l| (|e| (AA (NIL . 190685)))))
(|n| (AA (NIL . 157158) (NIL . 156650))
(|c| (|e| (AA (NIL . 157560)))))
(|r| (|y| (AA (NIL . 158038))))
(|t| (|e| (AA (NIL . 191195)))
(|i| (|o| (|n| (AA (NIL . 158519))))
(|v| (|e| (AA (NIL . 159006)))))
(|o| (|r| (AA (NIL . 159511)) (|y| (AA (NIL . 159989)))))))
(
|d|
(|o| (|m| (AA (NIL . 192104) (NIL . 191678)))))
... <etc> ...
The first list, (CL 3 0 UU), indicates that the associated
word-grammar works in ``unrestricted unification'' mode. This affects
how feature-sets are matched during parsing, and is described in [MA]. The second list names the corresponding entry file, and is
necessary so that the MA can tell on loading an index which file it
points into.
The remaining lines are the start of the index proper. The index entries
are sorted alphabetically. Amongst all the characters in citation forms,
the lowest-numbered is +, which starts all suffixes. This means
that the index starts with these: I showed the portion for the suffixes
able to dom. To finish, here is what the entry for able in the entries file looks like:
(|+able| |+able|
((INFL +) (BAR |-1|) (V +) (N +) (ADV -)
(AGR ((BAR |2|) (V -) (N +) (NFORM NORM))) (AFORM NONE)
(PART -) (NEG -) (QUA -) (NUM -) (AT +) (LAT +) (FIX SUF)
(GENINFL -) (STEM ((INFL +) (N -) (V +) (BAR |0|))))
ABLE NIL)
Presumably, this starts at position 190685 in the file.
It is not normally necessary to worry about how the index is stored,
because there are routines for accessing entries via it. However, some
knowledge is necessary if one intends to build other indexes, which we
do.
The above examples were printed from a lexicon built with the system
variables *print-pretty* set to T, and
*print-right-margin* set to 72. Normally, these are not set, and
the generated files are much harder to read. If you are debugging
software which uses these files, I recommend generating them in
pretty-print mode.
There are some Lisp implementations, such as DEC's Lisp, where the
built-in function file-position does not work. In DEC's case,
this is because if you can find out a file position, you should later be
able to return to it, and VMS makes that hard to achieve (actually it
isn't very hard, but harder than DEC were prepared to work). For such
systems, the MA allows an ``in-core'' flag to be set. This is done by
assigning to the MA global variable D-INCOREFLAG.
The normal setting is to the symbol |off|, returned by the
procedure DK-OFF. If you set it to |on|, returned by
calling the routine DK-ON, then the entries file will be left
empty. Instead of file-positions, the leaves of the index tree will be
the entries themselves.
Here is how the index shown above would start if the in-core flag
had been set on when compiling the lexicon:
(CL 3 0 UU)
(
|virreg-en.ma|
(
+
(
|a|
(|b| (|l| (|e| (AA (NIL |+able| |+able|
((INFL +) (BAR |-1|) (V +) (N +) (ADV -)
(AGR ((BAR |2|) (V -) (N +) (NFORM NORM)))
(AFORM NONE) (PART -) (NEG -) (QUA -) (NUM -)
(AT +) (LAT +) (FIX SUF) (GENINFL -)
(STEM ((INFL +) (N -) (V +) (BAR |0|))))
ABLE NIL)))))
(|n| (AA (NIL |+an| |+an|
((FIX SUF) (REG -) (INFL +) (BAR |-1|) (N +) (V -)
(POSS -) (PRO -) (PLU -) (NFORM NORM) (COUNT +)
(PER |3|) (NUM -) (AT +) (LAT +) (GENINFL -)
(STEM ((LAT +) (N +))))
AN NIL)
... <etc> ...
Note that the index still contains the name of the entries file, even
though that is irrelevant. If you compile a lexicon in in-core mode, the
entries file does get created, but remains empty.
When trying to understand the structure of a compiled lexicon, it's
important to realise that it will often contain more entries, or more
features in an entry, than the source form. This is because the user can
specify rules which generate new entries and features during
compilation. There are two types of rule, completion rules and
multiplication rules, both designed to alleviate the tedium of
writing the lexicon.
Completion rules add feature values. The rule below adds a BAR -1
feature-value pair to any entry which contains a FIX feature but
does not already contain a BAR feature.
Add_BAR_MINUS_ONE:
(_ _ ((FIX _fix) ~(BAR _) _rest) _ _) =>
(& & ((FIX _fix) (BAR -1) _rest) & &)
The part of the rule before the => is a pattern, specifying which
entries are to be added to. _fix is a variable which can match
any value. The ~ means not: only accept entries without a
BAR. The part of the rule after the arrow adds the feature-value
pair BAR -1, retaining all the features originally present.
Completion rules are described in section 8.6 of [MA]. Completion
rules can actually be used to delete or amend feature-value pairs as
well as adding them, by specifying a different value for some feature,
or not specifying it at all, in the second part of the rule. In
morphological generation, I use them to modify the entries for
inflectional affixes, as described in section 3.2.4.
Multiplication rules are described in section 8.7 of [MA].
Here is a multiplication rule:
MultRule1:
(_ _ ((V +) (N -) (BAR 0) (VFORM BSE) (INFL +) _rest) _ _) =>>
(
(& & ((V +) (N -) (BAR 0) (PN PER1) (INFL -) _rest) & &)
(& & ((V +) (N -) (BAR 0) (PN PER2) (INFL -) _rest) & &)
(& & ((V +) (N -) (BAR 0) (PN PLUR) (INFL -) _rest) & &)
)
What this does is to take an entry matching the pattern before the
arrow, and generate new entries from it. These new entries contain all
the features not mentioned explicitly in the pattern (symbolised by
_rest), as well as those that are. Thus, given the entry
(like lAIk ((BAR 0) (V +) (VFORM BSE) (N -) (INFL +) (SUBCAT VP2a))
LIKE NIL
)
the rule would create four new entries:
(like lAIk ((BAR 0) (V +) (VFORM BSE) (N -) (INFL +) (SUBCAT VP2a))
LIKE NIL
)
(like lAIk ((V +) (N -) (PN PER1) (BAR 0) (INFL -) (SUBCAT VP2a))
LIKE NIL
)
(like lAIk ((V +) (N -) (PN PER2) (BAR 0) (INFL -) (SUBCAT VP2a))
LIKE NIL
)
(like lAIk ((V +) (N -) (PN PLUR) (BAR 0) (INFL -) (SUBCAT VP2a))
LIKE NIL
)
I have not needed to use multiplication rules. However, it's necessary
to realise that they will generate new entries, and to plan for this if
modifying a lexicon or the MA. Note also that they can cause a lexicon
to grow enormously during compilation!
The information in the previous sections is necessary when
modifying the lexicon-handler, but contains more detail than needed for
a specification of irregular-form generation. This section ignores that
detail, and concentrates on the specification.
Abstractly, the lexicon can be viewed as a set of triples
< citation form, feature set, root form >
where the root form is the entry in the semantics field. The whole set
of entries can be regarded as a function 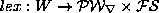 which maps the space
which maps the space 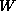 of words to a set of feature-set/root
pairs.
of words to a set of feature-set/root
pairs. 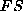 is the space of feature sets, and
is the space of feature sets, and 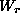 the set of roots.
the set of roots.
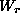 is a subset of
is a subset of 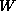 .
.
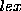 returns a set of answers because some citation forms correspond to
more than one feature-set/root pair. This is most obvious in cases such
as sheep, where we have one feature-set to indicate a singular
form and another to indicate the plural:
returns a set of answers because some citation forms correspond to
more than one feature-set/root pair. This is most obvious in cases such
as sheep, where we have one feature-set to indicate a singular
form and another to indicate the plural:
(sheep "" (N (COUNT +) (PLU +) (REG -)) SHEEP ())
(sheep "" (N (COUNT +) (REG -)) SHEEP ())
A more exotic case is abbot, which has one entry for the usual noun,
as in the abbot lived in the abbey, and another which (I think) is
for it as a form of address, as in the first occurrence in His title
was Abbot Francis James, and he was abbot of Liverpool. There is also
a third entry, whose purpose I don't know:
(abbot "" (N (COUNT +)) ABBOT ())
(abbot "" (N (COUNT +) (PREMOD +)) ABBOT ())
(abbot "" (N (ADDRESS +) (COUNT +)) ABBOT ())
Sometimes, the different entries are for different parts of speech.
Thus there is one entry for abandon as a noun - He danced with
great abandon - and two for it as a verb, as in The captain
should never abandon his ship.
(abandon "" (N (COUNT -)) ABANDON ())
(abandon "" (V (ARITY 2) (LAT -) (SUBCAT NP)) ABANDON ())
(abandon "" (V (ARITY 3) (LAT -) (PFORM TO) (SUBCAT NP_PP)) ABANDON ())
The three sets of entries above all come from the lexicon in
tex2html_html_special_mark_quot/home/projects2/edasst/ANLT3/dict/n.le" and v.le on the
Edinburgh cogsci machine.
In all these cases, the different entries still share the same root.
Abstractly, they are like this:
< w, fs1, r >
< w, fs2, r >
It is worth noting that the root is not marked to indicate which meaning
of a homonym is meant. Although the three abandons have different
meanings, the lexicon gives them both the same root; and this happens
for all the entries I have inspected.
There can also be cases where the same citation form maps to two
different roots:
< w, fs1, r1 >
< w, fs2, r2 >
This can happen if a word  is both an inflected form of one root, and
the uninflected form of another. One example is saw, which is both
the past tense of see, and the tool:
is both an inflected form of one root, and
the uninflected form of another. One example is saw, which is both
the past tense of see, and the tool:
(saw "" (N (COUNT +)) SAW ())
(saw "" (V (ARITY 1) (FIN +) (PAST +) (PRT OFF) (REG -)
(SUBCAT NULL))
SEE ()
)
Another is dug, which is both the past tense of dig, and a
word for teat or udder. The first two two entries were in the Edinburgh
lexicon; I haven't checked for the latter.
It might seem that yet another is digs: the third person singular
of dig, and the slang for lodgings. However, because the verb is
regular, it will not be in the lexicon, so the only entry would be for
the noun. Another example of this kind which I've found is fuller
as in Fuller's Earth, versus fuller meaning more full.
The MA defines a function D-Morpheme which implements 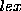 .
Calling
.
Calling
(D-Morpheme <citation form> )
will return a list of all the lexical entries matching the citation
form. D-Morpheme is described in section 3.1 of [MA].
This is essentially the task of inverting the function 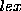 . We want to
define a function
. We want to
define a function 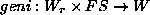 , which takes a root and
a feature set, and returns the corresponding irregular form. It has to
be assumed when implementing this that we have the root. For simple
words, it can easily be extracted from the parse-tree returned when the
word was originally analysed. For compound words the process is more
tricky, but is still feasible. Both cases are handled in
section 3.3.6; here, I'll assume the root is always
available, and that we're only dealing with simple words.
, which takes a root and
a feature set, and returns the corresponding irregular form. It has to
be assumed when implementing this that we have the root. For simple
words, it can easily be extracted from the parse-tree returned when the
word was originally analysed. For compound words the process is more
tricky, but is still feasible. Both cases are handled in
section 3.3.6; here, I'll assume the root is always
available, and that we're only dealing with simple words.
The first thing to check, before implementation, is whether it is
sensible to invert this function. Are there any tricky cases?
- Firstly, can
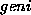 in fact be a function, in the sense that
it can only return one possible result? Can there be cases where it
could find more than one citation form for a given
root/feature-set pair? This could happen if the lexicon contained
two triples
in fact be a function, in the sense that
it can only return one possible result? Can there be cases where it
could find more than one citation form for a given
root/feature-set pair? This could happen if the lexicon contained
two triples
< w1, fs, r >
< w2, fs, r >
There are some cases in English where the same word can have both a
regular and an irregular form of the same syntactic type. The
plural of fish can be either fish or fishes. I think there
may be a subtle difference of meaning, but this would not be available
to the generator! The plural of grouse can be either grouses or
grouse. The first is where grouse means complaint or grievance:
The shop-steward invited all workers to voice their grouses against
the union. The second is where it refers to the bird.
Similar things can happen with verbs. Hang can have a regular
past-tense hanged: The executioner hanged the condemned man
at noon. It can also have an irregular form: I hung the poster on
my wall. The same happens with to lie: the politician lied
to the House; the drunk lay under the kebab van. The second
depends much more on meaning than the first, but again this is not
available to the generator. We have decided that in such cases, the
generator should return both possible forms.
In those cases, one form was regular, so this is outside the province of
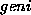 . I do not know whether the same root can have two different
irregular forms, but I haven't been able to think of any examples. I'll
assume however that it might happen. Formally, therefore,
. I do not know whether the same root can have two different
irregular forms, but I haven't been able to think of any examples. I'll
assume however that it might happen. Formally, therefore, 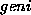 is a
function returning a set of words:
is a
function returning a set of words: 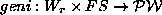 . For
further discussion, see section 3.7.
. For
further discussion, see section 3.7.
- Is
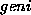 a total function? That is, is it defined no matter
what root/feature-set pair it is given?
a total function? That is, is it defined no matter
what root/feature-set pair it is given?
For roots, the answer is simple. We should only expect it to work if the
root is in the lexicon. This should always be the case if we stipulate
that the program calling 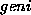 can never create new roots, but must
stick with those which have been derived by parsing a word.
can never create new roots, but must
stick with those which have been derived by parsing a word.
Within that constraint, 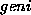 does require all irregular forms of
a word to be in the lexicon. If they are not, that is a fault in the
lexicon. However, it's not one that can be automatically detected.
does require all irregular forms of
a word to be in the lexicon. If they are not, that is a fault in the
lexicon. However, it's not one that can be automatically detected.
For feature sets, the answer is less clear. It's certainly possible to
construct feature-sets which will match more than one lexical entry. A
verb feature-set with no PAST feature would match both the
present and past tense of an irregular verb such as blow.
Unfortunately, it is possible that 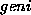 may get passed such sets, as
they won't come straight from the MA. Instead, they will have been
produced by the MA, then converted to the Assistant's representation,
then some components may have been discarded or changed, and then the
resulting set will have been converted back to the MA format. Because
the Assistant is still experimental, it is hard to know what will be
left in the sets it passes back. In addition, I have found that the
translation process does lose some features: see the comment on
structure fields in section
may get passed such sets, as
they won't come straight from the MA. Instead, they will have been
produced by the MA, then converted to the Assistant's representation,
then some components may have been discarded or changed, and then the
resulting set will have been converted back to the MA format. Because
the Assistant is still experimental, it is hard to know what will be
left in the sets it passes back. In addition, I have found that the
translation process does lose some features: see the comment on
structure fields in section  .
.
My pragmatic answer to this is that I shall allow 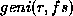 to match
more than one entry for
to match
more than one entry for  and
and 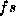 , as long as it only finds one
surface form. I have found that there are many occasions where the
lexicon has more than one entry for the same surface form and root, all
with slightly different feature-sets. For example, here is a selection
of feature-sets from the lexical entries for the surface form blew
of blow:
, as long as it only finds one
surface form. I have found that there are many occasions where the
lexicon has more than one entry for the same surface form and root, all
with slightly different feature-sets. For example, here is a selection
of feature-sets from the lexical entries for the surface form blew
of blow:
(V (AGR IT) (ARITY 0) (FIN +) (LAT -) (PAST +) (REG -)
(SUBCAT NULL))
(V (ARITY 1) (FIN +) (LAT -) (PAST +) (PRT ABOUT) (REG -)
(SUBCAT NULL))
(V (ARITY 1) (FIN +) (LAT -) (PAST +) (REG -) (SUBCAT NULL))
(V (ARITY 1) (FIN +) (PAST +) (PRT BACK) (REG -) (SUBCAT NULL))
(V (ARITY 1) (FIN +) (PAST +) (PRT DOWN) (REG -) (SUBCAT NULL))
and here is a selection for the surface form blow:
(V (AGR IT) (ARITY 0) (LAT -) (REG -) (SUBCAT NULL))
(V (ARITY 1) (LAT -) (PRT ABOUT) (REG -) (SUBCAT NULL))
(V (ARITY 1) (LAT -) (REG -) (SUBCAT NULL))
(V (ARITY 2) (LAT -) (REG -) (SUBCAT NP))
(V (ARITY 2) (ORDER FREE) (PRT DOWN) (REG -) (SUBCAT NP))
(V (ARITY 1) (PRT BACK) (REG -) (SUBCAT NULL))
Schematically, we have this situation:
< w1, fs11, r >
< w1, fs12, r >
< w1, fs13, r >
...
< w2, fs21, r >
< w2, fs22, r >
...
When called, 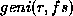 may match several triples. As long as they all
have the same
may match several triples. As long as they all
have the same  , I shall regard this as OK. However, if they match
more than one
, I shall regard this as OK. However, if they match
more than one  , I shall treat it as an error. This does not solve the
problem of words that genuinely have more than one irregular form: see
section 3.7.
, I shall treat it as an error. This does not solve the
problem of words that genuinely have more than one irregular form: see
section 3.7.
Given the stipulations above, the main task in generating irregular
forms is to build an index. We want to be able to look up, given a root
 and feature set
and feature set 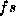 , all the feature-set/citation-form
combinations for that root. We then match
, all the feature-set/citation-form
combinations for that root. We then match 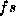 against each, and return
the corresponding citation forms.
against each, and return
the corresponding citation forms.
Luckily, the mechanisms for doing this are provided by the original
lexicon. Steve and I have modified the MA so that, when compiling
a lexicon, it builds two index files. One of them is the original
file, the one mapping citation forms to entries. It is stored in an
-le file, as mentioned in section 3.2.2.
The other, which I call the Irregular Forms Index, or IFI,
maps roots to entries. It is stored in a new file, whose name
ends in -ifi. In the original index, looking up a citation form
gives you a list of lexical entries for that form. In the IFI, looking
up a root gives you all the lexical entries which have that root in
their semantic field. So, abstractly, this implements a function 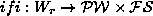 .
.
These modifications were made to D-MakeLexicon and subsidiary
functions. One change needed was to create a general indexing function,
(D-LookUpInIndex word fn index)
in AUTORUN.LSP. This searches for word in index,
and if found, applies fn to the result.
Before an IFI can be used, it must be loaded. This is done by calling
EA-LoadIFI, defined like the rest of the main morphological
generation stuff, in MORPHGEN.LSP. The original lexicon-loading
routine, D-LoadLexicon, does not load the IFI. (These comments
reflect the state of the MA as I write. The file MORPHGEN.LSP
will always contain up-to-date comments on any changes.)
To implement 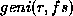 , we call
, we call 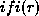 and then filter the
resulting entries against
and then filter the
resulting entries against 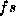 . If this filtering process produces more
than one citation form, we give an error, otherwise we return it. If it
produces none, we go on to try generating a regular form. (As mentioned
in section 3.7, this should be modified to handle the
possibilities of several irregular forms, of entries marked as having
regular and irregular forms, and of entries marked as never irregular.)
. If this filtering process produces more
than one citation form, we give an error, otherwise we return it. If it
produces none, we go on to try generating a regular form. (As mentioned
in section 3.7, this should be modified to handle the
possibilities of several irregular forms, of entries marked as having
regular and irregular forms, and of entries marked as never irregular.)
To filter the results of 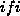 , I use feature-set unification. The
meaning of feature-set unification is described briefly in section 7.6
of [MA], and in more detail in section 7.4 of [G+M]. The MA
provides a function
, I use feature-set unification. The
meaning of feature-set unification is described briefly in section 7.6
of [MA], and in more detail in section 7.4 of [G+M]. The MA
provides a function D-Unify, used mainly in the parser, which
unifies two feature-sets. Is unification the right kind of matching?
This is difficult to answer, because it depends on how much information
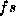 retains. Pragmatically, I think it is fair to stipulate that the
caller of
retains. Pragmatically, I think it is fair to stipulate that the
caller of 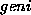 should arrange that his feature-sets be full enough
that unification will select only one surface form - though possibly
several lexical entries - in the sense of the previous section.
should arrange that his feature-sets be full enough
that unification will select only one surface form - though possibly
several lexical entries - in the sense of the previous section.
This section just gives a brief description of how to use
D-Unify, for anyone else who might need it. If you don't, skip
it. The routine, defined in MA file UNIFY, takes three arguments:
(D-Unify fs-1 b fs-2), where the first and third are feature-sets
represented as a list of lists. The second argument is a ``binding
list'', which specifies the values of any variables in the feature-sets.
D-Unify returns either the atom FAILED, or a list of the
form
( <new-fs> <new-bindings> )
The first element of this is the unification of fs-1 and
fs-2; the second element is a new binding list.
Feature-sets are represented as a list of lists, each inner list being a
pair
( <feature-name> <feature-value )
The value can be a symbol, a variable (see below), or another
feature-set.
A binding list is a list of pairs
( <variable> <value> )
Variables are represented as
( <number> <value-1> <value-2> ... )
where <number> is some kind of unique tag, and the values give
the variable's allowed range. Thus a variable which is allowed to range
over the values + and - might be represented as
(1 + -) or (13 - +). I don't think the values have to be
sorted in any way. Nor do they have to be the same as the range declared
for the feature they are unifying with. If you have declared PLU
as having range {+,-} in your feature declarations,
D-Unify will still happily unify the feature-set
( (PLU +) ) with ( (PLU (13 + 0) ). In fact,
D-Unify does not appear to use the declarations at all.
The last element of the binding list should, I think, always be
(T T). If the list contains no bindings at all, then it should be
((T T)).
Here is a sample call of D-Unify:
>(d-unify
'( (PLU +) )
'((t t))
'( (PLU (13 + -) ) (BAR |0|) )
)
(((BAR |0|) (PLU +)) (((13 + -) +) (T T)))
In irregular forms generation, both the feature-sets passed to
D-Unify will probably always be ground. Firstly, the one from the
lexical entry. The MA does allow the syntax field of a lexical entry to
contain variables (section 8.1 of [MA]), but none of the entries I
have seen in our lexica do.
Secondly, the one from which the irregular form is to be generated. As
far as I can make out from [MA], feature-sets returned from
D-LookUp and D-Morpheme will never contain unbound
variables unless the lexical entries from which they came do, or the
left-hand sides of the word-grammar rules do. Neither is true here. They
may contain ``don't-care'' values, symbols whose name starts with an
@D. These are added in response to the LCategory
definition: section 7.10 of [MA]. However, they are values, not
variables.
This means that we don't have to worry about variables, and can always
pass ((T T)) as our bindings list.



Next: Generating regular forms
Up: Implementing morphological generation within the MA
Previous: The exported routines
Jocelyn Ireson-Paine
Wed Feb 14 17:12:29 GMT 1996
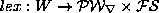 which maps the space
which maps the space 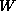 of words to a set of feature-set/root
pairs.
of words to a set of feature-set/root
pairs. 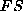 is the space of feature sets, and
is the space of feature sets, and 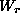 the set of roots.
the set of roots.
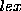 returns a set of answers because some citation forms correspond to
more than one feature-set/root pair. This is most obvious in cases such
as sheep, where we have one feature-set to indicate a singular
form and another to indicate the plural:
returns a set of answers because some citation forms correspond to
more than one feature-set/root pair. This is most obvious in cases such
as sheep, where we have one feature-set to indicate a singular
form and another to indicate the plural:
 is both an inflected form of one root, and
the uninflected form of another. One example is saw, which is both
the past tense of see, and the tool:
is both an inflected form of one root, and
the uninflected form of another. One example is saw, which is both
the past tense of see, and the tool:
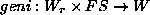 , which takes a root and
a feature set, and returns the corresponding irregular form. It has to
be assumed when implementing this that we have the root. For simple
words, it can easily be extracted from the parse-tree returned when the
word was originally analysed. For compound words the process is more
tricky, but is still feasible. Both cases are handled in
section
, which takes a root and
a feature set, and returns the corresponding irregular form. It has to
be assumed when implementing this that we have the root. For simple
words, it can easily be extracted from the parse-tree returned when the
word was originally analysed. For compound words the process is more
tricky, but is still feasible. Both cases are handled in
section 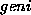 in fact be a function, in the sense that
it can only return one possible result? Can there be cases where it
could find more than one citation form for a given
root/feature-set pair? This could happen if the lexicon contained
two triples
in fact be a function, in the sense that
it can only return one possible result? Can there be cases where it
could find more than one citation form for a given
root/feature-set pair? This could happen if the lexicon contained
two triples
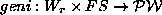 . For
further discussion, see section
. For
further discussion, see section 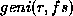 to match
more than one entry for
to match
more than one entry for  and
and 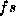 , as long as it only finds one
surface form. I have found that there are many occasions where the
lexicon has more than one entry for the same surface form and root, all
with slightly different feature-sets. For example, here is a selection
of feature-sets from the lexical entries for the surface form blew
of blow:
, as long as it only finds one
surface form. I have found that there are many occasions where the
lexicon has more than one entry for the same surface form and root, all
with slightly different feature-sets. For example, here is a selection
of feature-sets from the lexical entries for the surface form blew
of blow:
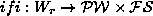 .
.
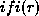 and then filter the
resulting entries against
and then filter the
resulting entries against 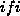 , I use feature-set unification. The
meaning of feature-set unification is described briefly in section 7.6
of [MA], and in more detail in section 7.4 of [G+M]. The MA
provides a function
, I use feature-set unification. The
meaning of feature-set unification is described briefly in section 7.6
of [MA], and in more detail in section 7.4 of [G+M]. The MA
provides a function