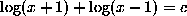PRESS

How PRESS worked:

Consider the following stages in solving .

1. .

2. .

3. .

4. .

5. .

6. .

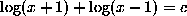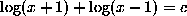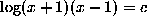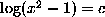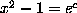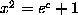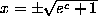In going from (3) to (6), we ``unwrap'' the at each stage, removing the dominant function on the left-hand side, and applying its inverse to the right-hand side. This method - Bundy calls it isolation - gradually decreases the ``depth'' of until it is completely isolated. It will always work if there is only one occurrence of , and the functions have inverses.

In going from (2) to (3), we reduce the number of 's. This - collection - is a necessary preliminary to isolation. We have to keep collecting 's until we only have one.

In going from (1) to (2), we can't collect the 's; they aren't close enough. Instead, we ``move them closer together''. Bundy calls this attraction.

So PRESS has the following structure:

solution( Lhs=Rhs, SolvedEquation ) :-
    occurrences_of( x, Lhs, 1 ),
    occurrences_of( x, Rhs, 0 ),
    isolate( Lhs=Rhs, SolvedEquation ).

solution( Equation, SolvedEquation ) :-
    occurrences_of( x, Equation, N ),
    N > 1,
    collect( Equation, Equation1 ),
    solution( Equation1, SolvedEquation ).

solution( Equation, SolvedEquation ) :-
    occurrences_of( x, Equation, N ),
    N > 1,
    attract( Equation, Equation1 ),
    solution( Equation1, SolvedEquation ).

Each of attract, collect, and isolate tries relevant algebraic transformations. For example:

attract( Equation, Equation1 ) :-
    sub_expression( E, Equation ),
    attract_rewrite( E, E1 ),
    replace_sub_expression( E, Equation, E1, Equation1 ).

attract_rewrite( log(U)+log(V), log(U*V) ) :-
    occurrences_of( x, U, NU ),
    NU > 0,
    occurrences_of( x, V, NV ),
    NV > 0.


collect( Equation, Equation1 ) :-
    sub_expression( E, Equation ),
    collect_rewrite( E, E1 ),
    replace_sub_expression( E, Equation, E1, Equation1 ).

collect_rewrite( (x+N)*(x-N), (x^2-N_squared) ) :-
    N_squared is N^2.


isolate( x=Rhs, x=Rhs ) :- !.

isolate( Equation, SolvedEquation ) :-
    isolate_rewrite( Equation, Equation1 ),
    isolate( Equation1, SolvedEquation ).

isolate_rewrite( log(A)=B, A=exp(B) ).
isolate_rewrite( A-X=B, A=X+B ).
isolate_rewrite( A^N=B, A=B^(1/N) ).