Uncomputable numbers and infinity




Next: About this document ...
Up: No Title
Previous: Uncomputable numbers
Back: to main list of student notes
Another way to see that some numbers are uncomputable is by pairing them
off against programs. Basically, there are more numbers than programs.
So there are some numbers that can't be produced by any program, i.e.
can't be computed.
To see this, number all programs, as in the previous section. Then say
that the  th program
th program  computes a real number
computes a real number  . Now, make a
number whose first digit is different from the first digit of the number
. Now, make a
number whose first digit is different from the first digit of the number
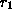 , i.e. whose first digit is different from that output by the first
program. Similarly, let its second digit be different from the second
digit of
, i.e. whose first digit is different from that output by the first
program. Similarly, let its second digit be different from the second
digit of 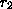 , i.e. from the second digit output by the second program.
No, since
, i.e. from the second digit output by the second program.
No, since  's first digit is different from that output by
's first digit is different from that output by 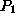 ,
,  is not the number that
is not the number that 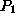 produces. Similarly, it isn't the number
that
produces. Similarly, it isn't the number
that 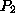 produces. And so on. So
produces. And so on. So  is a number that can't be
produced by any of our programs.
is a number that can't be
produced by any of our programs.

������������������������������������������������������������������������������������������������������������������������������������������������������




Next: About this document ...
Up: No Title
Previous: Uncomputable numbers
Back: to main list of student notes
Jocelyn Ireson-Paine
Wed Feb 14 23:47:23 GMT 1996
 th program
th program  computes a real number
computes a real number  . Now, make a
number whose first digit is different from the first digit of the number
. Now, make a
number whose first digit is different from the first digit of the number
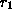 , i.e. whose first digit is different from that output by the first
program. Similarly, let its second digit be different from the second
digit of
, i.e. whose first digit is different from that output by the first
program. Similarly, let its second digit be different from the second
digit of 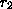 , i.e. from the second digit output by the second program.
No, since
, i.e. from the second digit output by the second program.
No, since  's first digit is different from that output by
's first digit is different from that output by 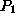 ,
,  is not the number that
is not the number that 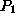 produces. Similarly, it isn't the number
that
produces. Similarly, it isn't the number
that 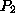 produces. And so on. So
produces. And so on. So  is a number that can't be
produced by any of our programs.
is a number that can't be
produced by any of our programs.