Some limits on neural networks - linear associator




Next: Some limits on neural networks - Hopfield net
Up: No Title
Previous: Introduction - The limits to computation
Back: to main list of student notes
In this section, I look at an example of a limit on what kinds of thing
can be learnt.
Linear associators are one of the simplest kinds of neural net, and
you've probably met them already. For those who haven't, here's a brief
description. See page 161 of Understanding Cognitive Science by
McTear (PSY KH:M 025) for a nice intro. Note that although I talk about
neurons and synapses, these nets (and indeed most connectionist models)
are not at all like real neurons.
Consider the following type of net. There are three inputs,  ,
,
 , and
, and  . There are three output neurons,
. There are three output neurons,  ,
,  , and
, and
 . Each input has synaptic connections to each of the three outputs.
Thus,
. Each input has synaptic connections to each of the three outputs.
Thus,  has one connection to
has one connection to  , another to
, another to  , and a third
to
, and a third
to  . The same for
. The same for  and
and  . Altogether, this gives nine
connections.
. Altogether, this gives nine
connections.
Each connection has a given numeric weight. In general, I'll use
 to denote the connection from
to denote the connection from  to
to  . Each output is
calculated as follows. Multiply each of the inputs by the corresponding
weight, and then add them. In symbols:
. Each output is
calculated as follows. Multiply each of the inputs by the corresponding
weight, and then add them. In symbols:

This architecture can be extended to any number, not just three. In
fact, the number of inputs does not need to be the same as the number of
outputs: the principles I describe below will still work. By setting the
weights suitably (``training'' the net), such nets can be trained to act
as recognisers, such that if you put pattern  in, you get a one on
in, you get a one on
 and zeros elsewhere; if you put pattern
and zeros elsewhere; if you put pattern  in, in, you get a one
on
in, in, you get a one
on  and zeros elsewhere; and so on.
and zeros elsewhere; and so on.
Question 1: assume we have a linear associator with two inputs and one
output. Can we train it to make the following association:

i.e. to give an output only when the inputs are the same? You may
recognise this as the ``exclusive-or'' problem.
Answer 1: No. All linear associators are what mathematicians call linear - hence the name. This means they obey two rules:
The input-output mappings in the exclusive-or table don't follow that
rule: hence we know the net can never produce them. Mathematically, the
net is a linear transformation (matrix) which acts on an input
vector to give an output vector. The only distinctions it can make are
those which are linearly separable.
The original Perceptron suffered from such a limitation, so you'll find
stuff about linear separability in most accounts of the Perceptron, e.g.
Introduction to the theory of neural computation by Herz et al
(PSY KH:H 044). You could not for example train the perceptron to
recognise all patterns containing exactly one dot while rejecting all
other images - see Crevier p 105.
Question 2: You read a paper whose author claims to have made a pattern
recogniser that gives the output  for the input
for the input  and gives
and gives 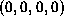 for every other input. He's done
this by connecting 37 linear associators in sequence. Do you believe
him?
for every other input. He's done
this by connecting 37 linear associators in sequence. Do you believe
him?
Answer 2: This is also impossible. If you connect any number of linear
associators together, the result is still linear (and can be
represented as just one associator).
 I once heard (maybe apocryphally) of an academic who wrote several
papers claiming to have implemented non-linear operations by combining
linear nets!
I once heard (maybe apocryphally) of an academic who wrote several
papers claiming to have implemented non-linear operations by combining
linear nets!




Next: Some limits on neural networks - Hopfield net
Up: No Title
Previous: Introduction - The limits to computation
Back: to main list of student notes
Jocelyn Ireson-Paine
Wed Feb 14 23:47:23 GMT 1996
 ,
,
 , and
, and  . There are three output neurons,
. There are three output neurons,  ,
,  , and
, and
 . Each input has synaptic connections to each of the three outputs.
Thus,
. Each input has synaptic connections to each of the three outputs.
Thus,  has one connection to
has one connection to  , another to
, another to  , and a third
to
, and a third
to  . The same for
. The same for  and
and  . Altogether, this gives nine
connections.
. Altogether, this gives nine
connections.
 to denote the connection from
to denote the connection from  to
to  . Each output is
calculated as follows. Multiply each of the inputs by the corresponding
weight, and then add them. In symbols:
. Each output is
calculated as follows. Multiply each of the inputs by the corresponding
weight, and then add them. In symbols:

 in, you get a one on
in, you get a one on
 in, in, you get a one
on
in, in, you get a one
on 
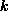 , then the
outputs will all be multiplied by
, then the
outputs will all be multiplied by 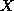 of outputs for a pattern
of outputs for a pattern 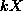 for
for 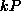 .
.
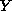 . Then for
inputs
. Then for
inputs 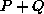 , we get outputs
, we get outputs 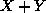 .
.
 for the input
for the input  and gives
and gives 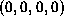 for every other input. He's done
this by connecting 37 linear associators in sequence. Do you believe
him?
for every other input. He's done
this by connecting 37 linear associators in sequence. Do you believe
him?