The board

In the previous section, you saw that Prolog can be used to navigate around structures defined by sets of facts. The following program navigates in a more literal sense. Please start by looking at the file entititled BOARD which comes with this supplement. It defines the basic predicates square, building, joins, in, loop, sells_fuel, buys and sells, plus three ones derived from them: adjacent, clockwise and distance.

Together, these describe a simple street layout, with squares containing shops and fuel stations. Unlike Monopoly, the squares are not confined to the outside of the board, but can form streets, some looped back on themselves, wandering over its interior.

More specifically, the predicates have the meanings given below:

• square(S,X,Y): S is the number of a square, lying at co-ordinate 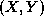. Each square has a unique number; these are integers (whole numbers), and work upwards from 1. Adjacent squares do not necessarily have adjacent numbers.

• building(S,B): B is the name of the building in square number S.

• joins(S1,S2): whereas square defines where squares lie and what they contain, joins defines how they are connected. There is one clause, joins(S1,S2) for every pair of connected squares. To make things simple, squares can only be connected by vertical, horizontal, or 45-degree diagonal lines.

• in(S,L): The board contains several streets that curve back on themselves, forming closed loops. Each loop has a name (you will see why later). There is one clause, in(S,L) for every square S that lies in a loop called L. You can think of the loops as being distinct regions of a city, such as the City in London or the central part of Oxford, except that to keep things simple, they do not contain any roads apart from the loop itself.

• loop(L): This defines the names of the loops. There is one clause for each loop.

• adjacent(S1,S2): This is true if S1 joins S2. Note that it is defined in terms of joins: S1 is next to S2 if S1 joins S2 or S2 joins S1. The reason for this is something we alluded to in the cave world example of Supplement 2. If Prolog has a fact such as

      joins(66,67).

  it does not automatically assume that the converse - joins(67,66) - is true. So we have to define a new predicate which holds no matter which way the squares are said to be joined. We could instead have had two sets of facts - both joins(66,67) and joins(67,66) - but this would waste space.

  The import of this is that if you want to find out about connected squares, you should use adjacent, not joins.

• clockwise(S1,S2): This is true if square S1 and S2 are both in the same loop, and S2 is immediately next to, and clockwise of, S1. Its purpose is to give you a simple way of finding your way round loops. It is defined in terms of joins, and only works because I took care, when generating the board definition, to make sure that the joins facts always had their arguments in an order which would make it work.

• distance(S1,S2,D): This sets D to the distance between S1 and S2. It uses is, an operator for doing arithmetic that you'll meet in Lesson 6. The formula is the standard one for working out distance in terms of X and Y co-ordinates: X^2 means X squared, and sqrt(...) means the square root of.

If you care to compare the BOARD file with the diagram of the board, it should become clear what these facts say.